上海浦东新区建平中学高中一年级（上）期中数学试题
1、填空题：（本大题共12小题，每小题3分，共36分）
1．设集合P={1，2，3，4}，Q={x|x≤2}，则P∩Q=__________．
2．集合{1，2，3}的真子集的个数为__________．
3．不等式
≥0的解集__________．
4．设α：x＞m，β：
1≤x＜3，若α是β的必要条件，则实数m的取值范围是__________．
5．已知a，b，c是实数，写出命题“若a+b+c=0，则a，b，c中至少有两个负数”的等价命题：__________．
6．若a＞0，b＞0，3a+2b=1，则ab的最大值是__________．
7．设全集U=R，A=
，则A∩（∁UB）=__________．
8．已知正数x，y满足
，则4x+9y的最小值为__________．
9．若不等式
的解集为（1，2），则实数a的值是__________．
10．关于x的不等式组
的解集不是空集，则实数a的取值范围为__________．
11．若A={x|mx2+x+m=0，m∈R}，且A∩R=∅，则实数m的取值范围为__________．
12．用M[A]表示非空集合A中的元素个数，记|A﹣B|=
，若A={1，2，3}，B={x||x2﹣2x﹣3|=a}，且|A﹣B|=1，则实数a的取值范围为__________．
2、选择题：（每小题4分，共16分）
13．假如a＜b＜0，那样下列不等式成立的是（）
A．
B．ab＜b2 C．﹣ab＜﹣a2 D．
14．已知a，b∈R+，那样“a2+b2＜1”是“ab+1＞a+b”的（）
A．充分非必要条件 B．必要不充分条件
C．充要条件 D．既不充分也非必要条件
15．不等式|x+1|﹣|x﹣2|≥a2﹣4a的解集为R，则实数a的取值范围是（）
A．（﹣∞，1]∪[3，+∞） B．（﹣∞，1）∪（3，+∞） C．[1，3] D．（1，3）
16．在下列条件中：①b2﹣4ac≥0；②ac＞0；③ab＜0且ac＞0；④b2﹣4ac≥0，＞0中能成为“使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件是（）
A．①②③ B．①②④ C．①③④ D．②③④
3、解答卷：本大题共5小题，共48分.解答应写出必要的文字说明或推理、验算过程.
17．解不等式组：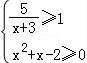
．
18．设全集U=R，集合A=
．
（1）求集合B；
（2）若A⊆（∁UB），求实数a的取值范围．
19．某化工厂生产某种商品，当年产量在150吨至250吨时，每年的生产本钱y万元与年产量x吨之间的关系可可近似地表示为y=
﹣30x+4000．
（1）若每年的生产总本钱低于2000万元，求年产量x的取值范围；
（2）求年产量为多少吨时，每吨的平均本钱最低，并求每吨的最低本钱．
20．已知M={x|1＜x＜3}，N={x|x2﹣6x+8≤0}．
（1）设全集U=R，概念集合运算△，使M△N=M∩（∁UN），求M△N和N△M；
（2）若H={x||x﹣a|≤2}，按（1）的运算概念求：（N△M）△H．
21．已知函数f（x）=ax2﹣2x+c，且f（x）＞0的解集是
．
（1）求f（2）的最小值及f（2）取最小值时f（x）的分析式；
（2）在f（2）获得最小值时，若对于任意的x＞2，f（x）+4≥m（x﹣2）恒成立，求实数m的取值范围．
2017-2018学年上海浦东新区建平中学高中一年级（上）期中数学试题
参考答案与考试试题分析
1、填空题：（本大题共12小题，每小题3分，共36分）
1．设集合P={1，2，3，4}，Q={x|x≤2}，则P∩Q=__________________________________________________．
【考试知识点】交集及其运算．
【剖析】由P与Q，求出两集合的交集即可．
【解答】解：∵P={1，2，3，4}，Q={x|x≤2}，
∴P∩Q={1，2}，
故答案为：{1，2}
2．集合{1，2，3}的真子集的个数为__________．
【考试知识点】子集与真子集．
【剖析】集合{1，2，3}的真子集是指是集合的部分组成的集合，包含空集．
【解答】解：集合的真子集为{1}，{2}，{3}，{1，2}，{1，3}，{2，3}，∅．共有7个．
故答案为7．
3．不等式
≥0的解集__________
______________________________．
【考试知识点】其他不等式的解法．
【剖析】依题意可得
①或
②，分别解之，取并即可．
【解答】解：∵≥0，
∴①或②
解①得：x∈∅；
解②得：＜x≤1，
∴不等式≥0的解集为（，1]．
故答案为：（，1]．
4．设α：x＞m，β：
1≤x＜3，若α是β的必要条件，则实数m的取值范围是______________________________．
【考试知识点】必要条件、充分条件与充要条件的判断．
【剖析】依据充分必要条件的概念与集合的包括关系求出m的范围即可．
【解答】解：α：x＞m，β：
1≤x＜3，
若α是β的必要条件，
则m＜1，
故答案为：（﹣∞，1）．
5．已知a，b，c是实数，写出命题“若a+b+c=0，则a，b，c中至少有两个负数”的等价命题：______________________________________________________________________．
【考试知识点】命题的真伪判断与应用．
【剖析】命题的逆否命题为若a，b，c中至多有1个非负数，则a+b+c≠0，即可得出结论．
【解答】解：命题的逆否命题为若a，b，c中至多有1个非负数，则a+b+c≠0，
故答案为若a，b，c中至多有1个非负数，则a+b+c≠0．
6．若a＞0，b＞0，3a+2b=1，则ab的最大值是__________
__________．
【考试知识点】基本不等式．
【剖析】借助基本不等式的性质即可得出．
【解答】解：a＞0，b＞0，3a+2b=1，
∴1=3a+2b≥2，当且仅当a=
，b=
时取等号，
∴ab≤，
∴ab的最大值是，
故答案为：
7．设全集U=R，A=
，则A∩（∁UB）=______________________________________________________________________________________________________________．
【考试知识点】交、并、补集的混合运算．
【剖析】解不等式求出集合A、B，依据补集与交集的概念写出A∩（∁UB）．
【解答】解：全集U=R，A={x|＜1}={x||x﹣1|＞1}={x|x＜0或x＞2}；
B={x|x2﹣5x+4＞0}={x|x＜1或x＞4}，
∴∁UB={x|1≤x≤4}，
∴A∩（∁UB）={x|2＜x≤4}．
故答案为：{x|2＜x≤4}．
8．已知正数x，y满足，则4x+9y的最小值为__________．
【考试知识点】基本不等式．
【剖析】将足代入所求关系式，借助基本不等式即可求得答案．
【解答】解：（4x+9y）（+
）=4+9+
+
≥13+2
=25，当且仅当x=
，y=时取等号，
故4x+9y的最小值为25
故答案为：25
9．若不等式的解集为（1，2），则实数a的值是__________
__________．
【考试知识点】其他不等式的解法．
【剖析】由题意可得原不等式为（x﹣1）（x﹣
）＜0，即可求出a的值．
【解答】解：等价于
﹣1＞0，等价于＞0，等价于（x﹣1）[（a﹣1）x+1]＞0，
∵不等式的解集为（1，2），
∴原不等式为（x﹣1）（x﹣）＜0，
∴=2，
解得a=，
故答案为：
10．关于x的不等式组
的解集不是空集，则实数a的取值范围为__________________________________________________．
【考试知识点】其他不等式的解法．
【剖析】分类讨论，即可求出a的取值范围
【解答】解：依据题意，x﹣a＜0的解为x＜a，
当a＞0时，ax＜1的解为x＜，
此时解集显然不为空集，
当a=0时，ax＜1的解为R，
此时解集显然不为空集，
当a＜0时，ax＜1的解为x＞，
∵关于x的不等式组的解集不是空集，
∴≤a，
即a2≤1，
解得﹣1≤a＜0，
综上所述a的取值范围为[﹣1，+∞）
故答案为：[﹣1，+∞）．
11．若A={x|mx2+x+m=0，m∈R}，且A∩R=∅，则实数m的取值范围为__________________________________________________________________________________________．
【考试知识点】交集及其运算．
【剖析】由已知得mx2+x+m=0无解，从而，由此能求出实数m的取值范围．
【解答】解：∵A={x|mx2+x+m=0，m∈R}，且A∩R=∅，
∴mx2+x+m=0无解，
∴，
解得m＜﹣或m＞．
∴实数m的取值范围是（﹣∞，﹣）∪（，+∞）．
故答案为：（﹣∞，﹣）∪（，+∞）．
12．用M[A]表示非空集合A中的元素个数，记|A﹣B|=
，若A={1，2，3}，B={x||x2﹣2x﹣3|=a}，且|A﹣B|=1，则实数a的取值范围为______________________________________________________________________．
【考试知识点】子集与交集、并集运算的转换．
【剖析】依据已知条件容易看出a=0符合，a＞0时，由集合B得到两个方程，x2﹣2x﹣3﹣a=0或x2﹣2x﹣3+a=0．容易看出B有2个或4个元素，所以辨别式△=4﹣4（a﹣3）＜0或△=4﹣4（a﹣3）＞0，如此即可求出a的范围．
【解答】解：（1）若a=0，得到x2﹣2x﹣3=0，∴集合B有2个元素，则|A﹣B|=1，符合条件|A﹣B|=1；
（2）a＞0时，得到x2﹣2x﹣3=±a，即x2﹣2x﹣3﹣a=0或x2﹣2x﹣3+a=0；
对于方程x2﹣2x﹣3﹣a=0，△=4+4（3+a）＞0，即该方程有两个不同实数根；
又|A﹣B|=1，B有2个或4个元素；
∴△=4﹣4（a﹣3）＜0或△=4﹣4（a﹣3）＞0；
∴a＜4或a＞4．
综上所述0≤a＜4或a＞4．
故答案为：0≤a＜4或a＞4．
2、选择题：（每小题4分，共16分）
13．假如a＜b＜0，那样下列不等式成立的是（）
A．
B．ab＜b2 C．﹣ab＜﹣a2 D．
【考试知识点】不等关系与不等式．
【剖析】因为a＜b＜0，可以令a=﹣2，b=﹣1，代入每个选项检验，只有D正确，从而得出结论．
【解答】解：因为a＜b＜0，可以令a=﹣2，b=﹣1，可得
=﹣1，∴
，故A不正确．
可得ab=2，b2=1，∴ab＞b2，故B不正确．
可得﹣ab=﹣2，﹣a2=﹣4，∴﹣ab＞﹣a2，故C不正确．
故选D．
14．已知a，b∈R+，那样“a2+b2＜1”是“ab+1＞a+b”的（）
A．充分非必要条件 B．必要不充分条件
C．充要条件 D．既不充分也非必要条件
【考试知识点】必要条件、充分条件与充要条件的判断；不等关系与不等式．
【剖析】本题考查的是必要条件、充分条件与充要条件的判断问题．在解答时，要先判断准条件和结论并分别是什么．然后结合不等式的常识分别由条件推结论和由结论推条件，看是不是正确即可获得问题解答．
【解答】解：由题意可知：a，b∈R+，若“a2+b2＜1”
则a2+2ab+b2＜1+2ab+a2•b2，
∴（a+b）2＜（1+ab）2
∴ab+1＞a+b．
若ab+1＞a+b，当a=b=2时，ab+1＞a+b成立，但a2+b2＜1不成立．
综上可知：“a2+b2＜1”是“ab+1＞a+b”的充分非必要条件．
故选A．
15．不等式|x+1|﹣|x﹣2|≥a2﹣4a的解集为R，则实数a的取值范围是（）
A．（﹣∞，1]∪[3，+∞） B．（﹣∞，1）∪（3，+∞） C．[1，3] D．（1，3）
【考试知识点】绝对值不等式的解法；函数恒成立问题．
【剖析】令f（x）=|x+1|﹣|x﹣2|，通过对x的取值范围的讨论，去掉绝对值符号，可求得f（x）min=﹣3，依题意，即可求得实数a的取值范围．
【解答】解：令f（x）=|x+1|﹣|x﹣2|，
当x＜﹣1时，f（x）=﹣1﹣x﹣（﹣x+2）=﹣3；
当﹣1≤x≤2时，f（x）=1+x﹣（﹣x+2）=2x﹣1∈[﹣3，3]；
当x＞2时，f（x）=x+1﹣（x﹣2）=3；
∴f（x）min=﹣3．
∵不等式|x+1|﹣|x﹣2|≥a2﹣4a的解集为R，
∴a2﹣4a≤f（x）min=﹣3，即实数a的取值范围是[1，3]．
故选C．
16．在下列条件中：①b2﹣4ac≥0；②ac＞0；③ab＜0且ac＞0；④b2﹣4ac≥0，＞0中能成为“使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件是（）
A．①②③ B．①②④ C．①③④ D．②③④
【考试知识点】必要条件、充分条件与充要条件的判断．
【剖析】依据二次方程ax2+bx+c=0的两根为正数，则肯定满足b2﹣4ac≥0，ab＜0，ac＞0，故依据必要不充分条件的概念即可判断．
【解答】解：∵二次方程ax2+bx+c=0的两根为正数，
∴b2﹣4ac≥0，ab＜0，ac＞0，
故由使二次方程ax2+bx+c=0的两根为正数，肯定能推出b2﹣4ac≥0，ab＜0，ac＞0，
但满足其中一个或2个不可以推出使二次方程ax2+bx+c=0的两根为正数，
故①②③能成为使二次方程ax2+bx+c=0的两根为正数”的必要非充分条件，
故选：A
3、解答卷：本大题共5小题，共48分.解答应写出必要的文字说明或推理、验算过程.
17．解不等式组：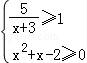
．
【考试知识点】其他不等式的解法．
【剖析】把要解的不等式组等价转化为
，从而求得它的解集．
【解答】解：不等式组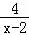：，即，即
，
求得﹣3＜x≤﹣2，或1≤x≤2，
故原不等式组的解集为{x|﹣3＜x≤﹣2，或1≤x≤2}．
18．设全集U=R，集合A=
．
（1）求集合B；
（2）若A⊆（∁UB），求实数a的取值范围．
【考试知识点】并集及其运算．
【剖析】（1）借助分式不等式的性质能求出集合B．
（2）由A={x|a﹣1＜x＜a+1}，CUB={x|2≤x＜5}，A⊆（∁UB），能求出实数a的取值范围．
【解答】解：（1）∵全集U=R，集合A=
．
∴集合B={x|
}={x|x＜2或x≥5}．
（2）∵A={x|a﹣1＜x＜a+1}，CUB={x|2≤x＜5}，A⊆（∁UB），
∴
，解得3≤a≤4．
∴实数a的取值范围是[3，4]．
19．某化工厂生产某种商品，当年产量在150吨至250吨时，每年的生产本钱y万元与年产量x吨之间的关系可可近似地表示为y=﹣30x+4000．
（1）若每年的生产总本钱低于2000万元，求年产量x的取值范围；
（2）求年产量为多少吨时，每吨的平均本钱最低，并求每吨的最低本钱．
【考试知识点】函数模型的选择与应用．
【剖析】（1）由题意可得不等式﹣30x+4000≤2000，解得即可．
（2）借助总本钱除以年产量表示出平均本钱，借助基本不等式求出平均本钱的最小值．
【解答】解：（2）由题意可得﹣30x+4000≤2000，解得100≤x≤200，
∵当年产量在150吨至250吨时，每年的生产本钱y万元与年产量x吨之间的关系
可近似地表示为y=﹣30x+4000，
∴150≤x≤200，
故每年的生产总本钱低于2000万元，年产量x的取值范围为[150，200]；
（2）依题意，每吨平均本钱为（万元），
则=+
﹣30≥2
﹣30=10
当且仅当x=200时取等号，又150＜200＜250，
所以年产量为200吨时，每吨平均本钱最低，每吨的最低本钱10万元．
20．已知M={x|1＜x＜3}，N={x|x2﹣6x+8≤0}．
（1）设全集U=R，概念集合运算△，使M△N=M∩（∁UN），求M△N和N△M；
（2）若H={x||x﹣a|≤2}，按（1）的运算概念求：（N△M）△H．
【考试知识点】交、并、补集的混合运算．
【剖析】（1）解不等式求出M，N，结合题意计算即可；
（2）解不等式求出集合H，结合（1）中N△M，分类讨论，可得（N△M）△H．
【解答】解：（1）M={x|1＜x＜3}，N={x|x2﹣6x+8≤0}={x|2≤x≤4}；
依据题意，U=R，∁UN={x|x＜2或x＞4}，
∴M△N=M∩（∁UN）={x|1＜x＜2}，
又∁UM={x|x≤1或x≥3}，
∴N△M=N∩（∁UM）={x|3≤x≤4}；
（2）∵H={x||x﹣a|≤2}=[a﹣2，a+2]，
∴（N△M）△H=（N△M）∩（CUH）=（1，2）∩[（﹣∞，a﹣2）∪（a+2，+∞）]，
当a﹣2≥2，或a+2≤1，即a≥4，或a≤﹣1时，（N△M）△H=（1，2）；
当1＜a﹣2＜2，即3＜a＜4时，（N△M）△H=（1，a﹣2）；
当1＜a+2＜2，即﹣1＜a＜0时，（N△M）△H=（a+2，2）；
当a﹣2≤1，且a+2≥2，即0≤a≤3时，（N△M）△H=∅．
21．已知函数f（x）=ax2﹣2x+c，且f（x）＞0的解集是
．
（1）求f（2）的最小值及f（2）取最小值时f（x）的分析式；
（2）在f（2）获得最小值时，若对于任意的x＞2，f（x）+4≥m（x﹣2）恒成立，求实数m的取值范围．
【考试知识点】二次函数的性质．
【剖析】（1）依据已知函数f（x）=ax2﹣2x+c，且f（x）＞0的解集为{x|x≠
}，可以函数开口向上，与x轴有一个交点，从而求解；
（2）由（1）求出f（x）的分析式，对于任意的x∈（2，+∞），f（x）+4≥m（x﹣2）恒成立，借助常数离别法，可以将问题转化为[（x﹣2）+]min≥m在x∈（2，+∞），恒成立，从而求出m的范围．
【解答】解：（1）由题意可得 ⇒ac=1⇒c＞0
所以f（2）=4a﹣4+c≥2
﹣4=0，
当且仅当4a=c即
时“=”成立，
由a=，c=2得：f（x）=x2﹣2x+2；
（2）由（1）可得f（x）=x2﹣2x+2=（x﹣2）2，
由于对于任意的x∈（2，+∞），f（x）+4≥m（x﹣2）恒成立，
∴m≤（x﹣2）+在x∈（2，+∞），恒成立，
故[（x﹣2）+]min≥m即可，
又函数y=（x﹣2）+在x∈（2，+∞）上递增，
所以[（x﹣2）+]min=2，
当且仅当x=2+2时“=”成立，
∴m≤2
；
